개발자 크루
내가 푼 문제를 저장하는 기능이 있음 좋겠어요!
푼 문제 저장하기

[21년 재직자 대회 예선] 이미지 프로세싱
- 난이도
- 3 단계
- 참가자
- 1 명
- 제출
- 1 명
- 정답률
- 100.00 %
언어별 시간/메모리
| 언어 | 시간 | 메모리 |
|---|---|---|
| JavaScript | 2초 | 1024MB |
| C | 2초 | 1024MB |
| C++ | 2초 | 1024MB |
| Java | 2초 | 1024MB |
| Python | 2초 | 1024MB |
자율주행 자동차를 구현하는 데에 있어서 이미지 프로세싱은 아주 중요한 요소이다. 카메라를 통해 들어온 차량 전후의 모습을 파악해 차량 근처에 있는 장애물들을 빠른 속도로 파악하고, 이를 다른 센서로부터 들어온 데이터와 함께 분석해 차량에게 올바른 명령을 내려야 하기 때문이다. 이 문제에서는 간단한 이미지 프로세싱을 하고자 한다.
H×W 크기의 2차원 비트맵 이미지가 있다. 이 이미지는 H×W개의 픽셀들로 구성되어 있으며, 위에서부터 i (1 ≤ i ≤ H)번째에 있고 왼쪽에서부터 j (1 ≤ j ≤ W)번째에 있는 픽셀은 (i, j)로 표기할 수 있다. 각 픽셀에는 색상이 붙어 있으며, 이 색상은 1 이상 109 이하의 정수로 표기할 수 있다. 픽셀 (i, j)의 색을 Ci, j라고 하자. 이 이미지에 아래와 같은 연산을 Q번 수행할 것이다:
(i, j, c): 픽셀 (i, j)를 고른다. 이 픽셀과 색깔이 같으면서 가로세로로 연결되어 있는 모든 픽셀들을 선택한 뒤, 그 픽셀들의 색을 모두 c로 바꾼다.
예를 들어 아래와 같은 이미지가 있다고 하자.
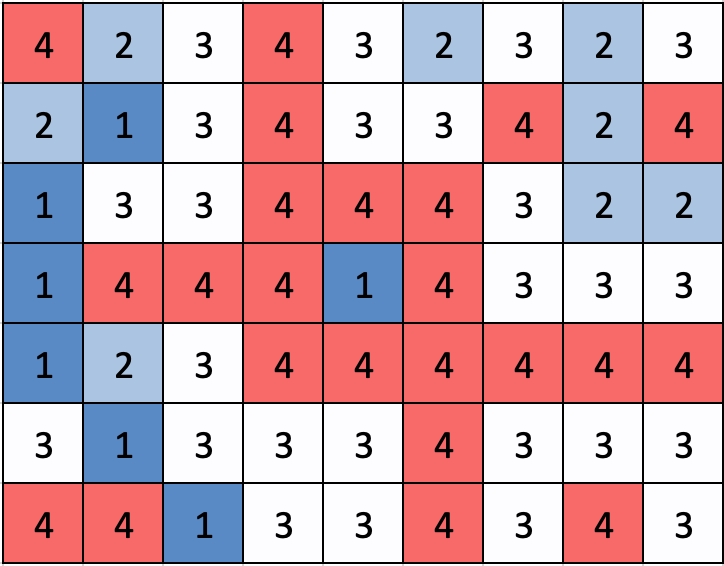
이 상황에서 (3,5,3) 연산을 수행해 보자. (3,5) 픽셀은 아래와 같다.
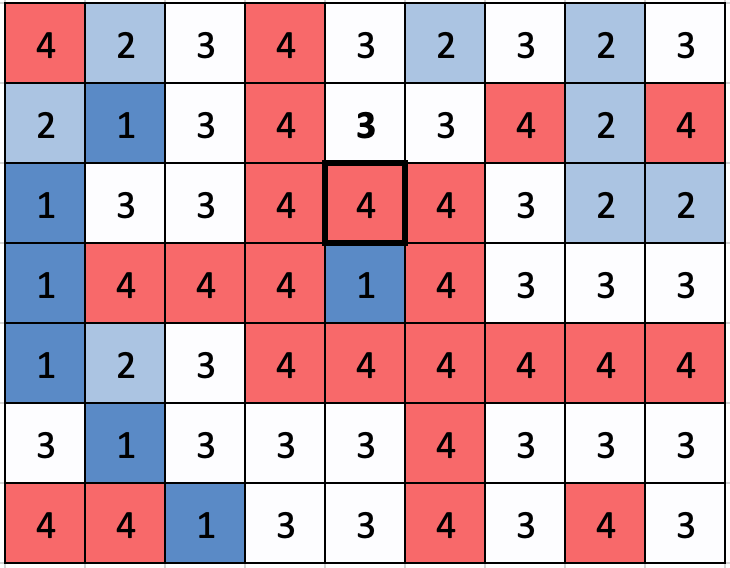
이 픽셀의 색은 4이므로, 색이 4이면서 (3,5)와 가로세로로 연결되어 있는 픽셀들을 선택하면 아래와 같다.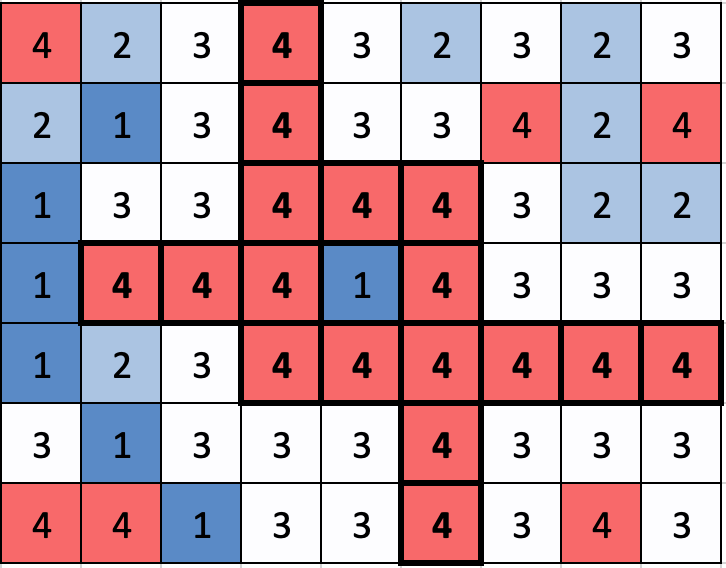
이 픽셀들의 색을 모두 3으로 바꾸면 된다.
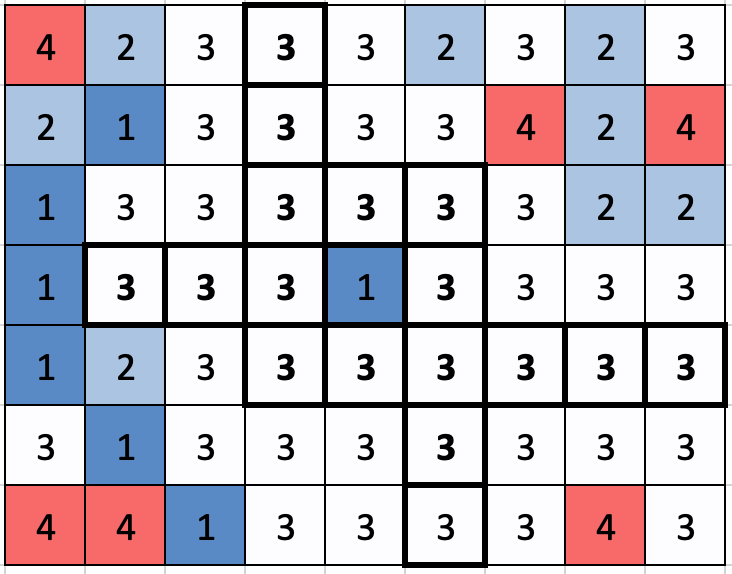
다음 연산을 수행한다면 위와 같이 이미지가 변경된 상태에서 반복적으로 수행할 것이다. 모든 연산을 수행한 뒤의 이미지를 출력하는 프로그램을 작성하라.
제약조건
1 ≤ H ≤ 128
1 ≤ W ≤ 128
모든 i, j (1 ≤ i ≤ H, 1 ≤ j ≤ W) 에 대해:
1 ≤ Ci, j ≤ 109
1 ≤ Q ≤ 500
각 연산 (i, j, c)에 대해:
1 ≤ i ≤ H
1 ≤ j ≤ W
1 ≤ c ≤ 109
주어지는 모든 수는 정수이다.
입력형식
첫 번째 줄에 두 정수 H와 W가 공백 하나를 사이로 두고 주어진다. 다음 H개의 줄에는 각 픽셀의 색상이 주어진다. 이 중 i (1 ≤ i ≤ H)번째 줄의 j (1 ≤ j ≤ W)번째 정수는 Ci, j이다.
그 다음 줄에는 Q가 주어진다. 다음 Q개의 줄에는 연산들이 순서대로 주어진다. 각 줄에는 세 개의 정수 i, j, c가 공백 하나를 사이로 두고 주어진다.
출력형식
모든 연산을 완료한 후, 최종 이미지를 H개의 줄에 W개의 정수를 공백 하나씩을 사이로 두고 출력한다.
입력예제1
1 9 1 1 2 2 2 1 1 2 2 2 1 5 1 1 5 2
출력예제1
2 2 2 2 2 2 2 2 2
입력예제2
7 9 4 2 3 4 3 2 3 2 3 2 1 3 4 3 3 4 2 4 1 3 3 4 4 4 3 2 2 1 4 4 4 1 4 3 3 3 1 2 3 4 4 4 4 4 4 3 1 3 3 3 4 3 3 3 4 4 1 3 3 4 3 4 3 1 3 5 3
출력예제2
4 2 3 3 3 2 3 2 3 2 1 3 3 3 3 4 2 4 1 3 3 3 3 3 3 2 2 1 3 3 3 1 3 3 3 3 1 2 3 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 4 4 1 3 3 3 3 4 3
입력예제3
7 9 4 2 3 4 3 2 3 2 3 2 1 3 4 3 3 4 2 4 1 3 3 4 4 4 3 2 2 1 4 4 4 1 4 3 3 3 1 2 3 4 4 4 4 4 4 3 1 3 3 3 4 3 3 3 4 4 1 3 3 4 3 4 3 4 3 5 3 1 9 2 3 9 3 3 9 1
출력예제3
4 2 1 1 1 2 1 1 1 2 1 1 1 1 1 4 1 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 4 4 1 1 1 1 1 4 1
