연습문제

[한양대 HCPC 2023] 활자 그래프

난이도
Lv. 4
제출
32 명
참가자
5 명
정답률
13.33 %
지원 언어
C
C++
Java
Python
JavaScript
언어별 시간/메모리
언어별 시간/메모리 표
언어 시간 메모리
C 2초 1024MB
Java 4초 1024MB
Python 6초 1024MB
C++ 2초 1024MB
JavaScript 6초 1024MB

고려 시대의 학자 하의비는 금속 활자를 사용해서 그래프를 찍어 내는 작업을 하고 있었다. 그러던 중, 하의비는 활자로 찍어내던, 일명 활자 그래프에서의 최단 경로가 궁금해졌다.


하의비는 현재 T개의 활자 그래프를 가지고 있으며, 만든 순서대로 1번부터 T번까지의 번호가 매겨져 있다.


 t번 활자 그래프는 Nt개의 번호가 붙은 정점으로 이루어져 있으며, 각각의 정점에는 1 이상 Nt 이하의 번호가 붙어있다. 이후, 다음과 같이 번호가 붙은 정점들 사이에 간선이나 이전에 만들었던 활자 그래프를 찍어내는 방식으로 t번 활자 그래프가 완성된다.


- 간선을 찍는 경우, v번 정점에서 w번 정점으로 가는 가중치가 있는 단방향 간선을 추가한다.

-  i번째 활자 그래프를 찍는 경우, i번째 활자 그래프의 시작점과 끝점이 t번 활자 그래프의 v번 정점과 w번 정점이 되도록 i번째 활자 그래프의 정점과 간선을 추가한다. 이 과정에서 생기는 i번째 활자 그래프의 정점들에는 번호가 붙지 않는다. (1 ≤ i < t) 


모든 활자 그래프의 시작점은 1번 정점이고, 끝점은 2번 정점이다.


이때, T번 활자 그래프의 1번 정점에서 2번 정점으로 가는 최단 경로를 구해 보자.

제약조건

1 ≤ T ≤ 100,000

2 ≤ Nt ≤ 200,000

0 ≤ Mt ≤ 500,000

번호가 붙은 정점의 개수의 합은 200,000을 넘지 않으며, 간선이나 다른 활자 그래프를 찍은 횟수의 합은 500,000을 넘지 않는다.

입력형식

첫 번째 줄에 활자 그래프의 개수 T가 주어진다.

이후, 각각의 활자 그래프에 대한 정보가 다음과 같이 주어진다.

  • 현재 t번 활자 그래프를 입력받는다고 해보자.
  • 첫 번째 줄에는 t번 활자 그래프의 번호가 붙은 정점의 개수 Nt와 간선이나 다른 활자 그래프를 찍은 횟수 Mt가 공백으로 구분되어 주어진다.
  • 이후 Mt개의 줄에 걸쳐 3개의 정수 v,w,x가 공백으로 구분되어 주어진다. (1 ≤ v,w ≤ Nt; v ≠ w; −(t−1) ≤ x ≤ 109)
    x ≥ 0이라면, 이는 v번 정점에서 w번 정점으로 가는 가중치 x의 단방향 간선을 찍었음을 의미한다.
    x < 0이라면, 이는 v번 정점을 시작점에 맞추고 w를 끝점에 맞춰서 |x|번 활자 그래프를 찍었음을 의미한다.

출력형식

첫 번째 줄에 T번 활자 그래프에서, 1번 정점에서 2번 정점으로 가는 최단 경로를 출력한다. 만약 1번 정점에서 2번 정점으로 가는 경로가 없거나, 이 값이 1018보다 크다면 −1을 대신 출력한다.

입력예제1

2
4 5
1 3 5
1 4 2
4 3 2
3 2 3
4 2 7
5 7
1 3 4
3 4 2
4 1 6
3 5 3
4 5 8
3 2 -1
5 2 7
출력예제1

11

1번 활자 그래프는 다음과 같이 생겼다.




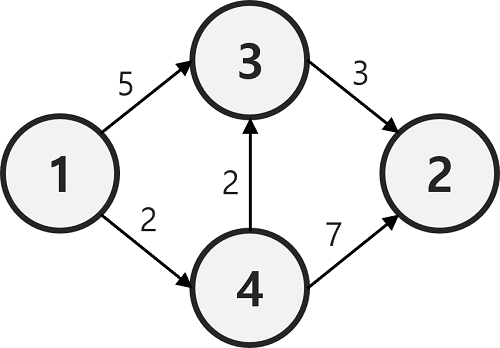
1번 활자 그래프가 사용된 2번 활자 그래프는 다음과 같이 생겼다.




2번 활자 그래프에서 1번 정점에서 2번 정점으로 가는 최단 경로는 11이 된다.

입력예제2

1
2 1
2 1 1
출력예제2

-1

입력예제3

1
2 0
출력예제3

-1

목록